Question

A box contains eighteen $1 bills, ten $5 bills, eight $10 bills, three $20 bills, and one $100 bill. You blindly reach into the box and draw a bill at random What is the expected value of your draw? The expected value of the draw is $ (Round to the nearest cent.)

Answer 1

Answer: $7.70

Explanation:

Given : A box contains eighteen $1 bills, ten $5 bills, eight $10 bills, three $20 bills, and one $100 bill.

Total bills =
`18+10+8+3+1=40`

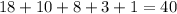
We know that probability of any event =
`\frac{\text{Favorable outcomes}}{\text{Total outcomes}}`

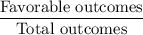
i.e. the probability of getting $1 bills =
`P(E_1)=(18)/(40)=0.45`

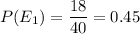
Probability of getting $10 bills =
`P(E_2)=(10)/(40)=0.25`

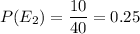
Probability of getting $5 bills =
`P(E_3)=(8)/(40)=0.2`

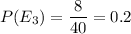
Probability of getting $20 bills =
`P(E_4)=(3)/(40)=0.075`

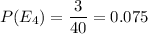
Probability of getting $100 bills =
`P(E_5)=(1)/(40)=0.025`

`\text{Expected value =}1* P(E_1)+5* P(E_2)+10* P(E_3)+20* P(E_4)+100* P(E_5)\\\\=1* 0.45+5* 0.25+10*0.2+20* 0.075+100* 0.025\\\\=7.7`

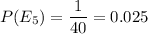
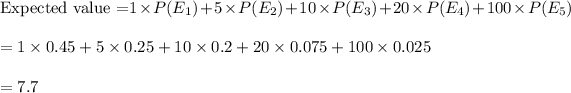
Hence, the expected value of your draw= $7.70