Answer:
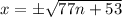
Explanation:
We have been given an equivalence equation
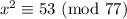 . We are asked to find all the square root of the given equivalence equation.
. We are asked to find all the square root of the given equivalence equation.
Upon converting our given equivalence equation into an equation, we will get:
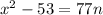
Add 53 on both sides:
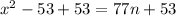
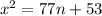
Take square root of both sides:
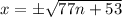
Therefore, the square root for our given equation would be
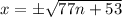 .
.