Question

Find the composition, Ro S, where S = {(1, a), (4, a),(5,6), (2, c), (3,c), (3, d)} with R = {(a,x), (a, y), (6, x), (c, z), (d, 2)} as a set of ordered pairs.

Answer 1

`R\circ S=\{(1,x),(1,y),(4,x),(4,y),(5,x),(2,z),(3,z),(3,2)\}`

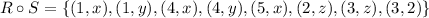
Explanation:

Given set of ordered pairs are

S = {(1, a), (4, a),(5,6), (2, c), (3,c), (3, d)}

R = {(a,x), (a, y), (6, x), (c, z), (d, 2)}

We need to find the composition
`R\circ S`.

If f(x) and g(x) are two functions, then

`(f\circ g)(x)=f(g(x))`

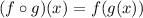
Elements S
`R\circ S`

1 a x

1 a y

4 a x

4 a y

5 6 x

2 c z

3 c z

3 d 2

The composition
`R\circ S` is defined as

`R\circ S=\{(1,x),(1,y),(4,x),(4,y),(5,x),(2,z),(3,z),(3,2)\}`

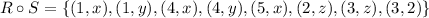
Therefore
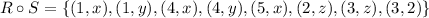`R\circ S=\{(1,x),(1,y),(4,x),(4,y),(5,x),(2,z),(3,z),(3,2)\}`.