Answer:
Mean = 38
Median = 38
Mode = 38
Range = 6
The variance is
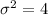
The standard deviation is

Explanation:
The mean is the sum of the values divided by the number of values. There are 8 values, so:
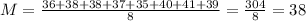
----------------
To find the median, the first step is to order the data set, so we have
35, 36,37,38,38,39,40,41
When n is even, as in this exercise, the median is the average of the values at the positions n/2 and (n+1)/2. Here, the value at position n/2, which is position 4, is 38. The value at position 5 is 38 to. The average between this values is (38+38)/2 = 38. So the median 38.
----------------------
The mode is the value that appears the most at the data set. 38 appears 2 times, while the other values appear once. So 38 is the mode.
-----------------
The range of a set is the result of the subtraction of the highest value by the lowest value of the set.
So, in this set:
Range = 41 - 35 = 6
-------------------
The variance of a N-cardinality set is given by the following formula:

where
 is the element at the position k of the set and M is the mean of the set.
is the element at the position k of the set and M is the mean of the set.
In our problem, we have that the variance is
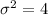 .
.
The standard deviation
 is the square root of the variance, so in our problem
is the square root of the variance, so in our problem
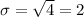 .
.