Question

16.4.57 Question Help A box contains eighteen $1 bills, ten $5 bills, eight $10 bills, three $20 bills, and one $100 bill You blindly reach into the box and draw a bill at random What is the expected value of your draw? The expected value of the draw is SL (Round to the nearest cent)

Answer 1

$ 7.7

Explanation:

Given,

There are 18 $1 bills, ten $5 bills, eight $10 bills, three $20 bills, and one $100 bill,

Total number of bills = 18 + 10 + 8 + 3 + 1 = 40,

`\because \text{Probability}=\frac{\text{Favourable outcomes}}{\text{Total outcomes}}`

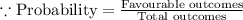
Thus,

The probability of $ 1 =
`(18)/(40)`

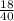
The probability of $ 5 =
`(10)/(40)`

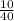
The probability of $ 10 =
`(8)/(40)`

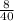
The probability of $ 20 =
`(3)/(40)`

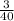
The probability of $ 100 =
`(1)/(40)`

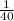
If a bill is selected randomly,

The expected value of the bill

`=(18)/(40)* 1+(10)/(40)* 5+(8)/(40)* 10+(3)/(40)* 20+(1)/(40)* 100`

`=(18+50+80+60+100)/(40)`

`=(308)/(40)`

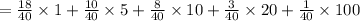
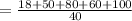
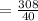
= $ 7.7