Answer with explanation:
Given : In a random sample of 200 drivers 18 years and older drawn in 2010, 58 of the drivers said they texted while driving.
i.e.
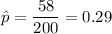
n= 200
Significance level :
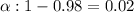
Critical value :
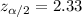
a) The confidence interval for population proportion is given by :-
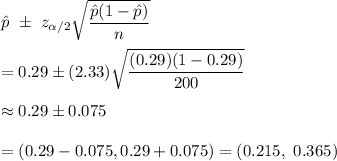
Hence, a 98% confidence interval to estimate the actual proportion has a lower limit of 0.215 and an upper limit of 0.365.
b). The margin of error for this sample :
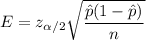
i.e.
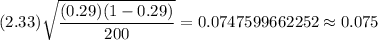
Hence, the margin of error for this sample is 0.075.