Question

A certain region would like to estimate the proportion of voters who intend to participate in upcoming elections. A pilot sample of 25 voters found that 21 of them intended to vote in the election. Determine the additional number of voters that need to be sampled to construct a 94​% interval with a margin of error equal to 0.04 to estimate the proportion. The region should sample additional voters.

Answer 1

Answer: 272

Explanation:

Given : A pilot sample of 25 voters found that 21 of them intended to vote in the election.

i.e.
`\hat{p}=(21)/(25)=0.84`

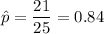
and the voters sampled = 25

Significance level :
`\alpha=1-0.94=0.06`

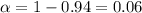
Critical value :
`z_(\alpha/2)=z_(0.03)1.88`

Margin of error: E = 0.04

The formula to find the sample size is given by :-

`n=\hat{p}(1-\hat{p})((z_(\alpha/2))/(E))^2\\\\\Rightarrow\ n=0.84(1-0.84)((1.88)/(0.04))^2\\\\=296.8896\approx297`

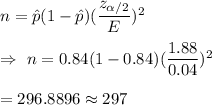
Then, the additional voters need to be sample =
`297-25=272`

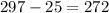
Hence, the region should sample 272 additional voters.