Question

Three chains attached to a metal ring are being pulled by different people. Christiane is exerting a force of 1200N at an angle of 30° to the horizontal and Hayley is exerting a force of 200N at an angle of 210° to the horizontal. What force and in which direction must Benjamin be exerting this force if the ring does not move? Round your answers to one decimal place.

Answer 1

Answer:1000 N

Explanation:

Given

Christiane is exerting a force of 1200 N at an angle of
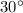`30^(\circ)` to the horizontal

Hayley exerting a force of 200 N at an angle of
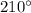`210^(\circ)` to the horizontal

Resolving Forces in horizontal and vertical direction

`R_x=1200cos\left ( 30\right )+200cos\left ( 210\right )+Fcos\theta`

`R_y=1200sin\left ( 30\right )+200sin\left ( 210\right )+Fsin\theta`

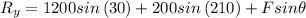
For Ring to remains in equilibrium

`R_x & R_y =0`

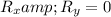
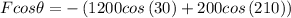`Fcos\theta =-\left ( 1200cos\left ( 30\right )+200cos\left ( 210\right )\right )`---1

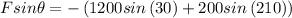`Fsin\theta =-\left ( 1200sin\left ( 30\right )+200sin\left ( 210\right )\right )`---2

Divide (1) & (2)

`tan\left ( \theta \right )=(\left ( 1200sin\left ( 30\right )+200sin\left ( 210\right )\right ))/(\left ( 1200cos\left ( 30\right )+200cos\left ( 210\right )\right ))`

`tan\left ( \theta \right )=(1)/(√(3))`

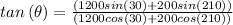
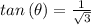
therefore
`\theta`is 30 or 210

but 30 is not possible therefore
`\theta` is 210

and magnitude of force will be

`Fcos210=-\left ( 1200cos\left ( 30\right )+200cos\left ( 210\right )\right )`

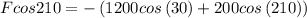
F=1000 N