Question

The annual interest rater, when compounded more than once a year, results in a slightly higher yearly interest rate. This is called the annual for effective) yield and denoted as Y. Find the annual yield as a percentage, given the annual interest rate and the compounding frequency Annual interest rate of 4.1%, compounded quarterly The effective annual yield is % (Type an integer or a decimal rounded to the nearest thousandth as needed.)

Answer 1

The effective annual yield is 4.163%.

Explanation:

Consider the provided information.

It is given that annual interest rate of 4.1%, compounded quarterly.

We will use n = 4.

It is also given that r = 4.1%

4.1% can be written as:

`(4.1)/(100)=0.041`

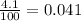
Now use the formula.

`y=(1+(r)/(n))^n-1`

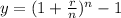
Now substitute the respective values in the above formula.

`y=(1+(0.041)/(4))^4-1`

`y=(1+0.01025)^4-1`

`y=(1.01025)^4-1`

`y=1.04163-1`

`y=0.04163=4.163\%`

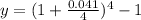
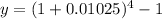
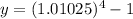
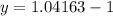
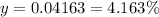
Hence, the effective annual yield is 4.163%.