Question

Consider a function f(x) = x^3*e^-2x defined for 0. Find the maximal value of this function and validate your solution using differentiation techniques.

Answer 1

The maximum value of the function is 0.168 at x=1.5.

Explanation:

The given function is

`f(x)=x^3e^(-2x)`

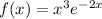
We need to find the maximal value of this function.

Differentiate the given function with respect to x.

`f'(x)=(d)/(dx)x^3e^(-2x)`

Product rule of differentiation:

`(d)/(dx)(fg)=fg'+f'g`

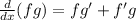
Using product rule, we get

`f'(x)=x^3(d)/(dx)e^(-2x)+e^(-2x)(d)/(dx)x^3`

`f'(x)=x^3e^(-2x)(-2)+e^(-2x)(3x^2)`

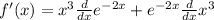
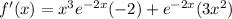
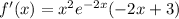`f'(x)=x^2e^(-2x)(-2x+3)` .... (1)

Equate f'(x)=0.

`0=x^2e^(-2x)(-2x+3)`

`x^2=0\Rightarrow x=0`

`e^(-2x)=0\Rightarrow \text{no solution}`

`-2x+3=0 \Rightarrow x=1.5`

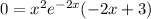
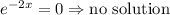
The function has two critical values 0 and 1.5.

Differentiate the f'(x) with respect to x.

`f''(x)=2 e^(-2 x) x (3 - 6 x + 2 x^2)`

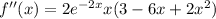
At x=0,

`f''(0)=2 e^(-2 (0)) (0)(3 - 6 (0) + 2*(0)^2)=0`

Since f''(0)=0, therefore x=0 is the point of inflection.

At x=1.5,

`f''(1.5)=2 e^(-2 (1.5)) (1.5)(3 - 6 (1.5) + 2*(1.5)^2)\approx-0.224`

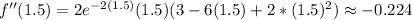
Since f''(1.5)<0, therefore the function is maximum at x=1.5.

Substitute x=1.5 in the given equation.

`f(1.5)=(1.5)^3e^(-2(1.5))`

`f(1.5)\approx 0.168`

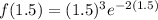
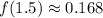
Therefore the maximum value of the function is 0.168 at x=1.5.