Answer: The verification is done below.
Step-by-step explanation: We are given to show that the function
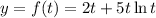 is a solution to the following differential equation :
is a solution to the following differential equation :

If
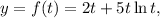 we have
we have

Therefore, we get
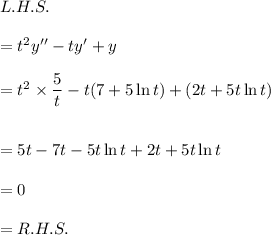
Thus, the function
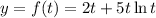 is a solution to the given differential equation.
is a solution to the given differential equation.
Hence showed.