Answer: (B) 32
Explanation:
Given expression :
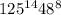
Since,
 and
and
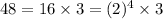
Now, the given expression can be written as :
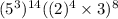
Since,
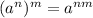
Then,

Since, 10 is divisible by 5 and 2 but not 3.
The greatest common number of values of 5 and 2 = 32
Then, the number of consecutive zeros would that integer have immediately to the left of its decimal point =32