Question

Find the least positive integer which gives remainder 1 when divided by 13, and remainder 2 when divided by 31.

Answer 1

The required integer is 157.

Explanation:

Let the unknown number be x.

It is given that the remainder 1 when x is divided by 13, and remainder 2 when x is divided by 31.

`x\equiv 1(mod 13)`

`x\equiv 2(mod 31)`

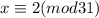
Here,
`a_1=1,a_2=2,n_1=13,n_2=31`

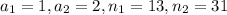
13 and 31 hare prime numbers. so the GCD o 13 and 31 is

`N=GCD(13,31)=13* 31=403`

`N_1=(N)/(13)=31`

`N_2=(N)/(31)=13`

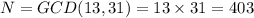
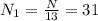
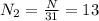
Using Chinese remainder theorem, we get

`y_1=31^(-1)(mod 13)=8`

`y_1=13^(-1)(mod 31)=12`

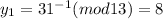
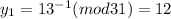
The formula to find the value of x is

`x\equiv (a_1y_1N_1+a_2y_2N_2)(mod N)`

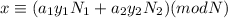
Substitute the given values in the above formula.

`x\equiv (1\cdot 8\cdot 31+2\cdot 12\cdot 13)(mod 403)`

`x\equiv 560(mod 403)`

`x=560+403n`

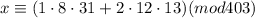
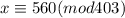
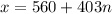
Let n=-1, because we need to find the least positive integer.

`x=560+403(-1)`

`x=560-403`

`x=157`

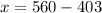
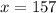
Therefore, the required integer is 157.