Answer:
The acceleration of the electron is 1.457 x 10¹⁵ m/s².
Step-by-step explanation:
Given;
initial velocity of the emitted electron, u = 1.5 x 10⁵ m/s
distance traveled by the electron, d = 0.01 m
final velocity of the electron, v = 5.4 x 10⁶ m/s
The acceleration of the electron is calculated as;
v² = u² + 2ad
(5.4 x 10⁶)² = (1.5 x 10⁵)² + (2 x 0.01)a
(2 x 0.01)a = (5.4 x 10⁶)² - (1.5 x 10⁵)²
(2 x 0.01)a = 2.91375 x 10¹³
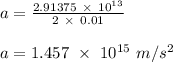
Therefore, the acceleration of the electron is 1.457 x 10¹⁵ m/s².