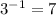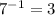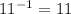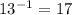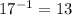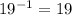Question

Make a list of all invertible elements of Z/20Z along with their inverses (under the multiplication operation).

Answer 1

Explanation:

We are given that
`(Z)/(20Z)`

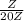
We have to find the invertible elements of
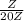`(Z)/(20Z)` along with their inverses under multiplication.

We know that

`(Z)/(20Z)^*\approx U(20)`

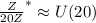
U(20)={1,3,7,9,11,13,17,19}

Operation used

`(a* b)/(20)=remainder`

Identity element=1

Inverse condition :
`a* a^(-1)=1`

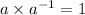
Inverse of 1=1

Inverse of 3

`3x=1mod (20)`

`3* 7=1mod(20)`

`(21-1)/(20)=(20)/(20)=0` (
`a=b mod n\implies (a-b)/(n)`)

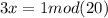
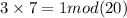
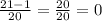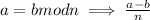Inverse of 3=7

Inverse of 7=3

Inverse of 9

`9x=1mod (20)`

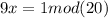
Inverse of 9 is 9 .

Inverse of 11

11 is also self inverse element.

`(13* 17)/(20)=1`

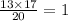
Where 1 is remainder

Hence inverse of 13 is 17 and inverse of 17 is 13.

19 is also self inverse element.

Therefore,

`1^(-1)=1`

`3^(-1)=7`

`7^(-1)=3`

`11^(-1)=11`

`13^(-1)=17`

`17^(-1)=13`

`19^(-1)=19`