Question

1a) For a spring with k = 20.0 N/m and hanging mass 100g, what is the angular frequency, w, of any simple harmonic oscillation process? b) For the spring system in question 1a, if you displace the hanging mass by 0.20 m and then allow the spring to oscillate, at what speed will the hanging mass pass the equilibrium position during each oscillation? You may assume that the spring is massless and is oscillating in a vacuum on the surface of the earth.

Answer 1

ω = 14.14 radian /s

2.82 ms⁻¹

Step-by-step explanation:

In a spring mass system the angular frequency is given by the expression

ω =
`\sqrt{(k)/(m) }`

Where k is spring constant which is given as 20 N/m and m is mass of the hanging mass which is given as .1 kg

Put the values in the given equation

ω =
`\sqrt{(20)/(.1) }`

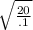
ω = 14.14 radian /s

b ) When displaced by .2 m and then allowed to oscillate it will do it with the amplitude A of 0.2 so

A = .2

Maximum velocity ie velocity at equilibrium will be equal to

ωA

= 14.14 X .2 = 2.82 ms⁻¹