Question

The distance from earth to the center of our galaxy is about 27,000 ly (1 ly = 1 light year = 9.47 × 10^15 m), as measured by an earth-based observer. A spaceship is to make this journey at a speed of 0.9990c. According to a clock on board the spaceship, how long will it take to make the trip? Express your answer in years. (1 yr is equal to 3.16 × 10^7 s.)

Answer 1

The time is 1206 years.

Step-by-step explanation:

Given that,

Distance = 27000 ly

`1\ ly =9.47*10^(15)\ m`

Speed = 0.9990c

We need to calculate the time

Using formula of speed

`v = (d)/(t)`

`t=(d)/(v)`

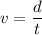
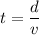
Put the value into the formula

`t =(27000*9.47*10^(15))/(3*10^(8))`

`t=8.523*10^(11)\ sec`

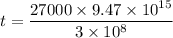
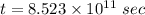
We need to calculate the time dilation the clock on the spaceship

Using formula of dilation time

`t'=t\sqrt{1-(v^2)/(c^2)}`

`t'=8.523*10^(11)*\sqrt{1-(( 0.9990c)^2)/(c^2)}`

`t'=8.523*10^(11)*√(1-(0.9990)^2)`

`t'=3.8106*10^(10)\ sec`

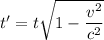
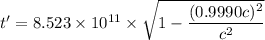
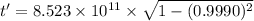
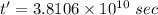
The time convert in years

We know that,

`1\ yr= 3.16*10^(7)\ sec`

So, the time is

`t'=(3.8106*10^(10))/(3.16*10^(7))`

`t'=1206\ years`

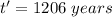
Hence, The time is 1206 years.