Question

Find the solutions to the quadratic. *
y = (x + 13)(x - 21)

Answer 1

`\huge\boxed{-13, 21}`

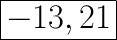
Explanation:

The most common way to solve for the roots of a polynomial is to use the Quadratic formula, which will return us with two values of x that make the equation equal 0.

...however, this form of the equation is already in root form. If we multiplied these two terms, we'd get
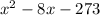`x^2 - 8x -273`, and when we factor that, we'd get -13 and 21.

Roots are usually written in the form
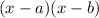`(x-a)(x-b)`, where the zeroes will be the value of x that makes each binomial equal 0 - aka, the opposite of a and b.

The opposite of 13 is -13, and the opposite of -21 is 21.

Therefore, the solutions of this equation are -13 and 21.

Hope this helped!