Answer:
proper time taken by the person is 9.911 × 10⁻⁵ s
Step-by-step explanation:
speed of the person in x- direction = 40,000 km/s
= 40,000 × 10³ m/s
= 4 × 10⁷ m/s
when the person just passes the street lamp is switched on which is at x =4 km
Lorentz factor =
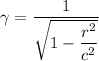
=
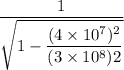
= 1.009
time taken in your frame of reference,t =
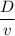
=
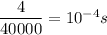
proper time =
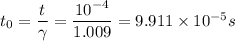
hence, proper time taken by the person is 9.911 × 10⁻⁵ s