Question

A laser used in eye surgery emits a 2.20-mJ pulse in 1.00 ns, focused to a spot 45.0 µm in diameter on the retina. (a) Find (in SI units) the power per unit area at the retina. (This quantity is called the irradiance.)

W/m^2
(b) What energy is delivered per pulse to an area of molecular size (say, a circular area 0.400 nm in diameter)?

Answer 1

(a). The power per unit area at the retina is
`13.8*10^(14)\ W/m^2`.

(b). The energy delivered per pulse to an area of molecular size is
`0.174*10^(-12)\ J`

Step-by-step explanation:

Given that,

Emitted energy = 2.20 mJ

Time t = 1.00 ns

Diameter D= 45.0 μm

Diameter of circular area d= 0.400 nm

(a). We need to calculate the power per unit area at the retina

Using formula of power

`Power\ per\ area = (E)/(t* A)`

`Power\ per\ area = (E)/(t* \pi r^2)`

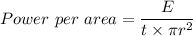
Put the value into the formula

`Power\ per\ area = (2.20*10^(-3))/(1.00*10^(-9)* \pi (22.5*10^(-6))^2)`

`Power\ per\ area = 13.8*10^(14)\ W/m^2`

(b). We need to calculate the energy is delivered per pulse to an area of molecular size

Using formula of energy

`E'=E*((d)/(D))^2`

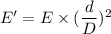
Put the value in to the formula

`E'=2.20*10^(-3)*((0.400*10^(-9))/(45.0*10^(-6)))^2`

`E'=1.738*10^(-13)\ J`

`E'=0.174*10^(-12)\ J`

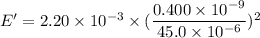
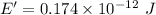
Hence, (a). The power per unit area at the retina is
`13.8*10^(14)\ W/m^2`.

(b). The energy delivered per pulse to an area of molecular size is
`0.174*10^(-12)\ J`