Question

A river has a steady speed of .9 m/s and is 150 m wide. A swimmer can swim 1.0 m/s in still water. The swimmer swims across the river and back taking the path which takes the least time. How far down river from the starting point does the swimmer land when she arrives back on the original bank?

Answer 1

Answer:270 m

Step-by-step explanation:

Given

River has a steady speed of 0.9 m/s and 150 wide

Swimmer speed in still water =1 m/s

In vector form

`V_r=0.9 \hat{i}`

`V_s=1\hat{j}`

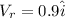
So if swimmer swim across the river then he will drifted away by some distance x because of the current of river

not net resultant velocity of swimmer

`=√(V_r^2+V_s^2)`

`=√(1^2+0.9^2)`

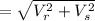
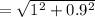
=1.345m/s

So swimmer will get deflected by

`tan\theta =(V_r)/(V_s)=(0.9)/(1)`

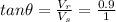
so get deflected by going

`tan\theta =(x)/(150)`

`x=150* 0.9=135`

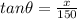
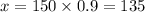
same deflection is observed while returning

Therefore total deflection is 135+135=270 m