Answer:
The distance is
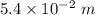 .
.
Step-by-step explanation:
Given that,
Spring constant = 670 N/m
Mass = 0.011 g
We know that,
The potential energy stored in a compressed spring is given by
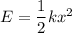 ....(I)
....(I)
We know that,
The equation of energy is
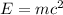 ....(II)
....(II)
We need to calculate the distance
Using equation (I) and (II)
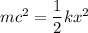
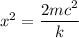
Where, m = mass
c = speed of light
k = spring constant
Put the value into the formula
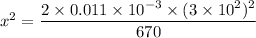
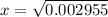
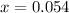

Hence, The distance is
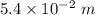 .
.