Question

A tire is rolling along a road, without slipping, with a velocity v. A piece of tape is attached to the tire. When the tape is opposite the road (at the top of the tire), its velocity with respect to the road is: A) 2v. B) zero. C) 1.5v. D) v. E) The velocity depends on the radius of the tire.

Answer 1

2V.

Step-by-step explanation:

We know rolling motion is superposition of rotational and translational motion.

Also, it is rolling without slipping.

Therefore,
`V=\omega * R` .....1

Where, V is linear velocity and
`\omega` is angular velocity of tire.

Now, at the top point :

Its, linear velocity is V because the tire it is moving with a velocity V.

Now , it is at a distance R from the center of tire.

Its , Velocity due to rotation
`V_r=\omega * R`. {because is is not slipping}.

Both these velocities are in same direction.

Therefore,
`V_t=V+V_r\\V_t=V+V=2V`

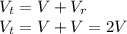
Because,
`V_r=V` ( from 1)

Hence, it is the required solution.

Answer 2

The correct answer is option 'a': 2v

Step-by-step explanation:

For a object under pure rolling the velocity of any point is given by

`v_(rolling)=v_(translational)+v_(rotational)`

Since in case of pure rolling the angular velocity is related to the transnational velocity as

`\omega =(v_(translational))/(r)`

positive value is taken as the velocities have the same direction.

Thus the rotational velocity is given by

`v_(rotational)=\omega * r\\\\\\v_(rotational)=(V_(trans))/(r)* r\\\\v_(rotational)=v_(trans)`

Thus the velocity at the tip becomes

`v_(rolling)=v+v\\\\v_(rolling)=2v`