Question

A cell phone is placed 25 cm in front of a diverging lens with focal length of magnitude 20 cm. How far is the image of this phone from the lens?

Answer 1

-11.11 cm

Step-by-step explanation:

The lens formula is defined as,

`(1)/(f)= (1)/(v)-(1)/(u)`

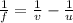
Here, f is the focal length, u is the distance of an object, v is the distance of image.

Given that, the diverging lens is given so according to sign convention of diverging less, u and f should be negative.

Given that, distance of an cell phone in front of a diverging lens is
`u=-25 cm`

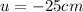
And its focal length is
`f=-20 cm`.

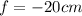Put the variables in lens formula. Therefore,

`(1)/(-20)= (1)/(v)-(1)/(-25)\\ (1)/(v)=(1)/(-20)-(1)/(25)\\ (1)/(v)=-((5+4)/(100)) \\v=-(100)/(9) \\ v=-11.11 cm`

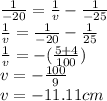
Therefore the image is formed of this phone at a distance of -11.11 cm from the lens.