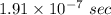Question

Photoelectrons from a material with a binding energy of 2.71 eV are ejected by 450 nm photons. Once ejected, how long (in s) does it take these electrons to travel 2.60 cm to a detection device?

Answer 1

The time is
`1.91*10^(-7)\ sec`

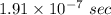
Step-by-step explanation:

Given that,

Energy = 2.71 eV

Length = 450 nm

Distance = 2.60 cm

We need to calculate the speed of photon

Using formula of photoelectric emission

`\phi+K.E=(hc)/(l)`

`(1)/(2)mv^2=(hc)/(l)-\phi`

`v^2=(2((hc)/(l)-\phi))/(m)`

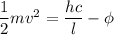
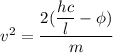
Where, K.E = kinetic energy

h = Planck constant

Put the value into the formula

`v^2=(2((6.63*10^(-34)*3*10^(8))/(450*10^(-9))-2.71*1.6*10^(-19)))/(9.1*10^(-31))`

`v=\sqrt{1.846*10^(10)}`

`v=1.358*10^(5)\ m/s`

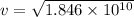
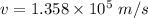
We need to calculate the time

Using formula of distance

`v = (d)/(t)`

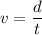
Put the value into the formula

`t = (d)/(v)`

`t=(2.60*10^(-2))/(1.358*10^(5))`

`t=1.91*10^(-7)\ sec`

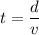
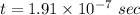
Hence, The time is
`1.91*10^(-7)\ sec`