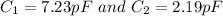Question

Two capacitors give an equivalent capacitance of 9.42 pF when connected in parallel and an equivalent capacitance of 1.68 pF when connected in series. What is the capacitance of each capacitor?

Answer 1

`C_1=7.23pF\ and\ C_2=2.19pF`

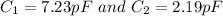
Step-by-step explanation:

Let the two capacitance are
`C_1\ and\ C_2`

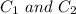
It is given that when capacitors are connected in parallel their equvilaent capacitance is 9.42 pF

So
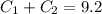`C_1+ C_2=9.2`--------EQN 1

And when they are connected in series their equivalent capacitance is 1.68 pF

So
`(1)/(C_1)+(1)/(C_2)=(1)/(1.68)`

`(C_1+C_2)/(C_1C_2)=(1)/(1.68)`

`C_1C_2=1.68* 9.42=15.8256pF`

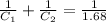
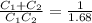
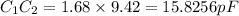
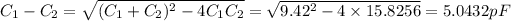`C_1-C_2=√((C_1+C_2)^2-4C_1C_2)=√(9.42^2-4* 15.8256)=5.0432pF`-----EQN

On solving eqn 1 and eqn 2

`C_1=7.23pF\ and\ C_2=2.19pF`