Answer:
Step-by-step explanation:
given,
tuning fork vibration = 508 Hz
accelerates = 9.80 m/s²
speed of sound = 343 m/s
observed frequency = 490 Hz

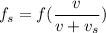
![v_s = v[(f_s)/(f_o)-1]](https://img.qammunity.org/2020/formulas/physics/college/dn3429iskvrybyqp3k7h4a87giu1dzrd4e.png)
![= 343[(508)/(490)-1]](https://img.qammunity.org/2020/formulas/physics/college/voeqyd5j0e705ae7kmhze1ms6iivrwhz9k.png)
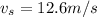
distance the tunning fork has fallen
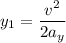
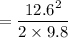
=8.1 m
now, time required for the observed will be
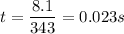
now, for the distance calculation
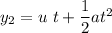
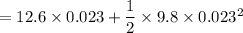
=0.293 m
total distance
= 8.1 + 0.293 = 8.392 m