Question

A photon of wavelength 7.33 pm scatters at an angle of 157° from an initially stationary, unbound electron. What is the de Broglie wavelength of the electron after the photon has been scattered?

Answer 1

4.63 p.m.

Step-by-step explanation:

The problem given here can be solved by the Compton effect which is expressed as

`\lambda^(')-\lambda=(h)/(m_e c)(1-cos\theta)`

here,
`\lambda` is the initial photon wavelength,
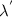`\lambda^(')` is the scattered photon wavelength, h is he Planck's constant,
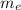`m_e` is the free electron mass, c is the velocity of light,
`\theta` is the angle of scattering.

Given that, the scattering angle is,
`\theta=157^(\circ)`

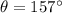
Putting the respective values, we get

`\lambda^(')-\lambda=(6.626* 10^(-34) )/(9.11* 10^(-31)* 3* 10^(8)  ) (1-cos157^\circ ) m\\\lambda^(')-\lambda=2.42* 10^(-12) (1-cos157^\circ ) m\\\lambda^(')-\lambda=2.42(1-cos157^\circ ) p.m.`

Therfore,

`\lambda^(')-\lambda=4.64 p.m.`

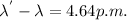
Here, the photon's incident wavelength is
`\lamda=7.33pm`

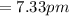
So,

`\lambda^(')=7.33+4.64=11.97 p.m`

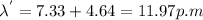
From the conservation of momentum,

`\vec{P_\lambda}=\vec{P_(\lambda^('))}+\vec{P_e}`

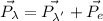
here,
`\vec{P_\lambda}` is the initial photon momentum,
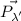`\vec{P_(\lambda^('))}` is the final photon momentum and
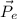`\vec{P_e}` is the scattered electron momentum.

Expanding the vector sum, we get

`P^2_(e)=P^2_(\lambda)+P^2_(\lambda^('))-2P_\lambda P_(\lambda^('))cos\theta`

Now expressing the momentum in terms of De-Broglie wavelength

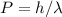`P=h/\lambda` and putting it in the above equation we get,

`\lambda_(e)=\frac{\lambda \lambda^(')}{\sqrt{\lambda^(2)+\lambda^(2)_(')-2\lambda \lambda^(') cos\theta}}`

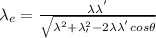
Therfore,

`\lambda_(e)=\frac{7.33* 11.97}{\sqrt{7.33^(2)+11.97^(2)-2* 7.33* 11.97* cos157^\circ }} p.m.\\\lambda_(e)=(87.7401)/(18.935) = 4.63 p.m.`

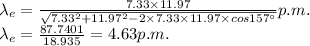
This is the de Broglie wavelength of the electron after scattering.