Answer:
The speed of the truck is 20.68 m/s.
Step-by-step explanation:
Given that,
Frequency of horn = 211 Hz
Trucker hears a frequency = 187 Hz
Speed of sound = 343 m/s
Let the speed of the truck is
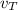
We need to calculate the speed of truck
Using Doppler shift
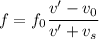
Where,
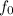 = horn frequency
= horn frequency
f = Trucker hears a frequency
v'=speed of sound
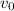 = speed of observer
= speed of observer
v = speed of source
Put the value in to the formula
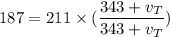
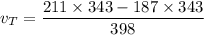
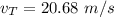
Hence, The speed of the truck is 20.68 m/s.