Question

You want to paint a piece of pottery at an art studio.The total cost is the cost of the price plus an hourly studio fee. There are two studios to choose from.

Answer 1

Part a) For 3 hours of painting the total costs are the same at both studios

Part b) The costs of both studios will never be the same, the cost of studio B will always be higher than the cost of studio A.

Explanation:

the complete question in the attached figure

Let

y ------> the total cost

x -----> the number of hours

we know that

The total cost is the cost of the piece of pottery plus the number of hours multiplied by an hourly studio fee

substitute the given values (see the attached figure)

Studio A

`y=8x+10` -----> equation A

Studio B

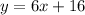`y=6x+16` -----> equation B

Part a) After how many hours of painting are the total costs the same at both studios?

Equate equation A and equation B and solve for x

`8x+10=6x+16`

`8x-6x=16-10`

`2x=6`

`x=3\ hours`

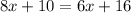
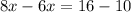
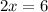
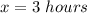
Verify the cost

studio A ----->
`y=8(3)+10=\$34`

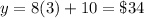
studio B ----->
`y=6(3)+16=\$34`

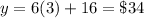
therefore

For 3 hours of painting the total costs are the same at both studios

Part b) Studio B increases the hourly studio fee by $2. How does this affect your answer in part a? Explain

we have that

Studio A

`y=8x+10` -----> equation A

Studio B

`y=(6+2)x+16`

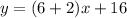
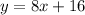`y=8x+16` -----> equation B

Equate equation A and equation B and solve for x

`8x+10=8x+16`

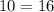`10=16` -----> is not true

The system has no solution

therefore

The costs of both studios will never be the same, the cost of studio B will always be higher than the cost of studio A.