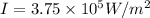Question

A krypton laser produces a cylindrical red laser beam 2.40 mm in diameter with 1.70 W of power. What is the light intensity 1.76 m away from the laser?

Answer 1

`I=3.75* 10^5 W/m^2`

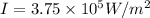
Step-by-step explanation:

Given that

Diameter of laser beam d= 2.4 mm

Radius of laser beam r= 1.2 mm

Power P =1.7 W

We know that intensity(I) of laser beam given as follows

`I=(P)/(\pi r^2)`

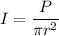
Now by putting the values

`I=(P)/(\pi r^2)`

`I=(1.7)/(\pi * 0.0012^2)`

So

`I=3.75* 10^5 W/m^2`

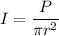
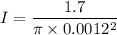
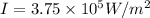
So the intensity at 1.76 m away from laser

`I=3.75* 10^5 W/m^2`