Question

An LC circuit consists of a capacitor with C = 2.9 μF and an inductor with L = 30 mH. At t = 0 the capacitor has charge 6.3 μC and the current in the inductor is zero. The circuit oscillates at its resonant frequency. How long after t = 0 will the current in the circuit be maximum?

What will be this maximum current?

Answer 1

0.02654618617 seconds

Step-by-step explanation:

`I=I_(max) sin(ωt-Φ)`

In this case you want to find the maximum current. So
`I=I_(max)`

`I/I_(max)=sin(ωt-Φ)` phi is 0

your resonance is going to be the capacitance and the inductance and then solve for t.
`sin^(-1)(1)=ωt`

Answer 2

Step-by-step explanation:

In the L-C oscillation , energy is transferred between capacitor and inductor with a certain periodicity.

Initial energy in the capacitor = 1/2X Q² / C

`((6.3*10^(-6))^2)/(2*2.9*10^(-6))`

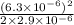
= 6.84 x 10⁻⁶ J

Initial energy of inductor is zero.

Total energy = 6.84 x 10⁻⁶ J

When all the energy is stored in the inductor , it has maximum current . Let this current be I

Energy of inductor

= 1/2 L I²

Here I is maximum current in the inductor.

Conserving energy

1\2 L I² = 6.84 X 10⁻⁶

.5 X 30 X 10⁻³ I² = 6.84 X 10⁻⁶

I = 2.13 X 10⁻²

= 21.3 mA.

Time period of oscillation

T =
`2\pi√(LC)`

=
`2 X 3.14 \sqrt{30*10^(-3)*2.9*10^(-6)}[`

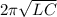
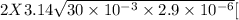
188.4 10^{-5}.s

Current will be maximum after 1/ 4 of time period

= .25 x 188.1 x 10⁻⁵ s

47 X 10⁻⁵ s