Question

Observer 1 rides in a car and drops a ball from rest straight downward, relative to the interior of the car. The car moves horizontally with a constant speed of 3.80 m/s relative to observer 2 standing on the sidewalk.

a) What is the speed of the ball 1.00 s after it is released, as measured by observer 2?

b) What is the direction of travel of the ball 1.00 s after it is released, as measured relative to the horizontal by observer 2?

Answer 1

a) 10.5 m/s

While for observer 1, in motion with the car, the ball falls down straight vertically, according to observer 2, which is at rest, the ball is also moving with a horizontal speed of:

`v_x = 3.80 m/s`

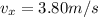
As the ball falls down, it also gains speed along the vertical direction (due to the effect of gravity). The vertical speed is given by

`v_y = u_y + gt`

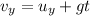
where

`u_y =0` is the initial vertical speed

g = 9.8 m/s^2 is the acceleration of gravity

t is the time

Therefore, after t = 1.00 s, the vertical speed is

`v_y = 0 + (9.8)(1.00)=9.8 m/s`

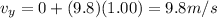
And so the speed of the ball, as observed by observer 2 at rest, is given by the resultant of the horizontal and vertical speed:

`v=√(v_x^2 +v_y^2)=√((3.8)^2+(9.8)^2)=10.5 m/s`

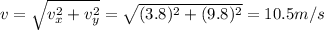
b)
`\theta = -68.8^(\circ)`

As we discussed in previous part, according to observer 2 the ball is travelling both horizontally and vertically.

The direction of travel of the ball, according to observer 2, is given by

`\theta = tan^(-1) ((v_y)/(v_x))=tan^(-1) ((-9.8)/(3.8))=-68.8^(\circ)`

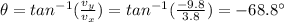
We have to understand in which direction is this angle measured. In fact, the car is moving forward, so
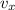`v_x` has forward direction (we can say it is positive if we take forward as positive direction).

Also, the ball is moving downward, so
`v_y` is negative (assuming upward is the positive direction). This means that the direction of the ball is forward-downward, so the angle above is measured as angle below the positive horizontal direction:

`\theta = -68.8^(\circ)`