Answer:
Part 1)
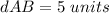
Part 2)
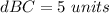
Part 3)
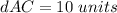
Part 4) In the explanation (The point B is between point A and point C)
Explanation:
we know that
the formula to calculate the distance between two points is equal to

we have
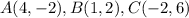
step 1
Find distance AB
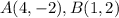
substitute the values in the formula
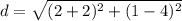
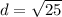
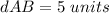
step 2
Find distance BC
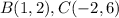
substitute the values in the formula
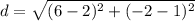
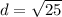
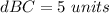
step 3
Find distance AC
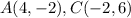
substitute the values in the formula
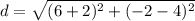
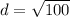
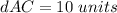
step 4
Prove that points A, B, and C are collinear. Which point is in between the other two?
we know that
If the points are collinear
then
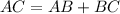
we have
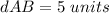
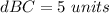
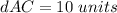
substitute
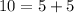
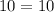 ----> is verified
----> is verified
The point B is between point A and point C