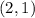Answer:
A) The coordinates of the fourth vertex are:
1) x-coordinate:
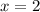
2) y-coordinate:
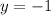
B) The point of intersection of the diagonals is:
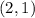
Explanation:
We need to remember that the diagonals of a parallelogram intersect each other at a half-way point and the midpoint of each diagonal is the same.
The midpoint formula is:
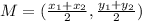
Since:
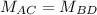
We can find the coordinates of the fourth vertex
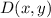 through these procedure:
through these procedure:
1) x-coordinate:
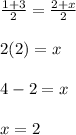
2) y-coordinate:
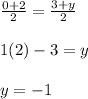
Therefore, fourth vertex is
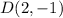
Since the point of intersection of the diagonals is the midpoint of a diagonal (Remember that
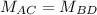 ), this is:
), this is:
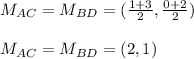
Therefore, the point of intersection of the diagonals is