Answer:
The total balance on December 1, 2016 is B = $7356.28
Explanation:
I am going to call B1 the balance for the first deposit, B2 the balance for the second deposit and B3 for the third deposit.
This is a compound interest problem.
The compound interest formula is given by:
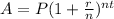
A: Amount of money(Balance)
P: Principal(Initial deposit)
r: interest rate(as a decimal value)
n: number of times that interest is compounded per unit t
t: time the money is invested or borrowed for.
First step: Balance B1 on December 1, 2016
A = amount of money = B1
P = 1,700
r = 0.056
n = 12(compounded mothly, and t is in years)
t = 8 years

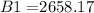
Second step: Balance B2 on December 1, 2016
A = B3
P = 1,700
r = 0.056
n = 12(compounded mothly, and t is in years)
t: From January 1, 2010 to December 1, 2016 there are 6 years and 11 months. 11 months is 0.92 of a year. So
t = 6.92
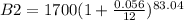
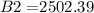
Third step: Balance B3 on December 1, 2016
A = B3
P = 1700
r = 0.056
n = 12
t: 4 years and 7 months. 7 months is 7/12 = 0.58. So t = 4.58 years.
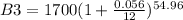
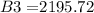
Final step: Total balance on December 1, 2016
B = 2195.72 + 2502.39 + 2658.17
B = $7356.28
So the total balance on December 1, 2016 is B = $7356.28