Answer:
The density of the ring is:
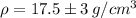
This means the ring could very well be made of gold, but it is very unlikely that it is made of brass.
Step-by-step explanation:
For a quantity f(x,y) that depends on other quantities (in this case two) x and y, the error is given by:
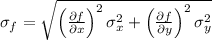
where
 and
and
 are the standard deviations on errors of the variables
are the standard deviations on errors of the variables
 and
and
 .
.
In our case
 where
where
 is the mass and
is the mass and
 is the volume.
is the volume.
Knowing that
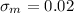 and
and
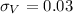 we can estimate the error on the density
we can estimate the error on the density
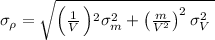
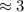 (values were directly plugged)
(values were directly plugged)
The density is by using the given values
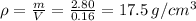
The density with error is given by

Which means it could go as high as 20.5 or as low as 14.5, Meaning that the ring could very well be made of gold, but it is very unlikely that it is made of brass.