Question

A car is traveling down the highway at speed v when the driver slams on the brakes and skids to a stop in a distance d. Assuming the same frictional force, how far would the car slide if its speed was 2v?

Answer 1

It would slide a distance 4d

Step-by-step explanation:

From the first scenario where the speed is v and the distance sliding is d we can calculate de value of the acceleration:

`V_(f)^(2) =V_(o)^(2) - 2.a.x`

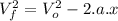
We know that

`V_(f)=0`

`V_(o)=v`

`x=d`

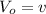
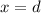
So, the acceleration is
`a=(v^(2))/(2d)`

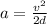
Now, using the same formula and with the new value for
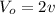`V_(o)=2v` we can solve for x from:

`0=(2v)^(2) -2.(v^(2))/(2d) .x`

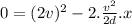
x=4d