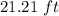Answer:
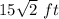 ≈
≈
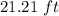
Explanation:
Observe the figure attached.
You need to use the following Trigonometric function in order to find the length of the diagonal "d":
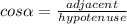
For this case:
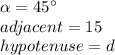
Therefore, you need to substitute these values into the Trigonometric function and solve for "d":
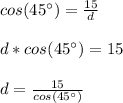
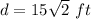 ≈
≈