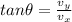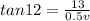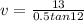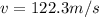Question

Two cars approach an extremely icy four-way perpendicular intersection. Car A travels northward at 26 m/s and car B is traveling eastward. They collide and stick together, traveling at 12o north of east. What was the initial velocity of car B? You may assume that the cars have the same mass. Round your answer to one decimal place.

Answer 1

`v = 122.3 m/s`

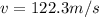
Step-by-step explanation:

As we know that momentum conservation is hold good when we consider elastic or inelastic collision between two objects

so here we have

`m_1v_(1i) + m_2v_(2i) = m_1v_(1f) + m_2v_(2f)`

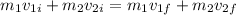
so here we have

`m(26 \hat j) + m(v \hat i) = (m + m)\vec v_f`

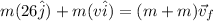
so we have

`\vec v_f = 0.5 v\hat i + 13\hat j`

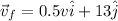
since we know that final velocity of two cars at 12 degree angle in North of East

so we will have

`tan\theta = (v_y)/(v_x)`

`tan12 = (13)/(0.5 v)`

`v = (13)/(0.5 tan12)`

`v = 122.3 m/s`