Step-by-step explanation:
The given data is as follows.
Half-life (
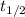 ) for
) for
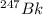 is
is
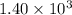 year
year
or,
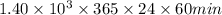 year
year
=
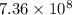 min
min
Relation between decay constant and half-life is as follows.
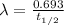
Therefore, putting the values into it we get the following.
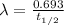
=

=
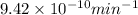
Since, it is given that mass of
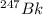 is 247.070 U. According to Avogadro's law, 247.070 g of
is 247.070 U. According to Avogadro's law, 247.070 g of
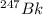 contains
contains
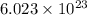 atoms of
atoms of
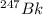 .
.
Hence, number of atoms present in 0.00456 g of
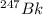 will be calculated as follows.
will be calculated as follows.
0.00456 g of
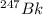 =
=
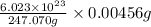
=
 atoms of
atoms of
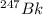
It is known that expression for decay rate is
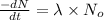
where,
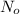 = no. of atoms present in given amount of substance
= no. of atoms present in given amount of substance
Hence,
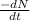 = 9.42 \times 10^{-10} min^{-1} \times 1.11 \times 10^{19}[/tex]
= 9.42 \times 10^{-10} min^{-1} \times 1.11 \times 10^{19}[/tex]
=
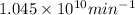
As each decay is emitting only one alpha particle.
Therefore, we can conclude that number of alpha particles emitted per minute will be
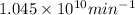 .
.