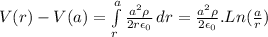Answer:
Step-by-step explanation:
I will use the Gauss's Law to find the field for both cases, after this I'll calculate the potential.
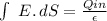
the surface S is an "infinite long" cylinderr of radio r, the normal vector only has radial coordinates.
E(r)=E(r)r /*The field, based on cylindrical symmetry, only depends of the radius, and only has radial coordinate*/
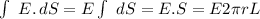
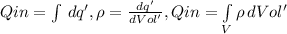
if r<a
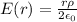 with radial versor
with radial versor
if r>=a the gaussian surface encloses all the charge, so
Qin=p.Vol=
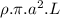
then:
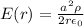 with radial versor.
with radial versor.
In the case when the cylinder has a hole, the field will be null there (because there is not charge inside the gaussian). to calculate the field I can suppose that in the hole I have an charge density -ρ, to cancel with the other.
Potential:
V(r)-V(a)=

if r<a
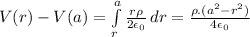
if r>a