Question

Find a nonzero vector that is perpendicular to both the vectors u = <2, 1, -1> and v = <2, 1, 1> use cross product to find

Answer 1

<2, -4, 0>

Step-by-step explanation:

Given vectors,

u = <2, 1, -1>

⇒ u = 2i + j - k

v = <2, 1, 1>

⇒ v = 2i + j + k

∵ The cross product of u and v is a orthogonal or perpendicular vector to both vectors u and v,

`\because u* v=\begin{vmatrix}i & j &k \\ 2 & 1 & -1\\ 2 & 1 & 1\end{vmatrix}`

`=i(1+1)-j(2+2)+k(2-2)`

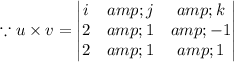
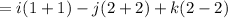
= 2i - 4j + 0k

Hence, the vector which is perpendicular to both u and v is <2, -4, 0>