Answer:
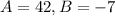
Explanation:
The current function of time is defined as follows:
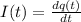
where
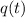 is the charge function.
is the charge function.
For the given charge function of time
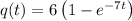 we have the following current function:
we have the following current function:
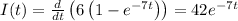
In the problem it is proposed that
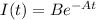 .
.
Examining the expression of
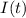 we obtained by deriving
we obtained by deriving
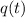 with the expression proposed by the problem and comparing term by term:
with the expression proposed by the problem and comparing term by term:
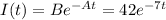
We conclude that
 and
and
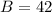 .
.