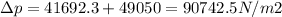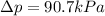Answer:
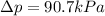
Step-by-step explanation:
specific gravity of oil is
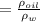
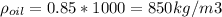
we know that
change in pressure for oil is given as
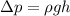
here density and h is for oil
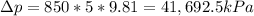
change in pressure for WATER is given as
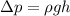
here density is for water and h is for water
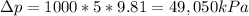
pressure change due to both is given as