Question

Your grandmother bought an annuity from Rock Solid Life Insurance Company for $200,000 when she retired. In exchange for the $200,000, Rock Solid will pay her $25,000 per year until she dies. The interest rate is 5%. How long must she live after the day she retired to come out ahead (that is, to get more in value than what she paid in)

Answer 1

The number of years she has to live to come out ahead is 11 (or 10.47 to be precise).

Step-by-step explanation:

We know that she breaks even the the net present value (NPV) is 0. Having the following data:

- Initial value (IV) = -$200,000

- Final value (FV) = 0

- Interest rate (r) = 5% = 0.05

- Payment (P) = $25,000

The formula for the number of years she must live to come out ahead (n) is given by:

`n = Log_(10)(P/(P+IV/ r))/Log_(10)(1+r)`

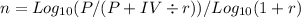
Replacing in the formula with the known values we have:

`n = Log_(10)(25000/(25000-200000/ 0.05))/Log_(10)(1+0.05) = 10.4698 \approx 11`

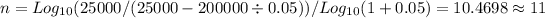
Therefore the number of years grandma has to live to come out ahead is 11 (or 10.4698 to be more precise).