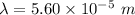Question

Determine the wavelength of a monochromatic beam of light that impinges on a double slit with a slit separation of 2.80 mm. Bright fringes are produced on a screen 1.20 m from the double slit. The brights are separated by .024m.

Answer 1

`\lambda=5.60* 10^(-5)\ m`

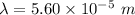
Step-by-step explanation:

For constructive interference, the expression is:

`d* sin\theta=m* \lambda`

Where, m = 1, 2, .....

d is the distance between the slits.

The formula can be written as:

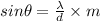`sin\theta=\frac {\lambda}{d}* m` ....1

The location of the bright fringe is determined by :

`y=L* tan\theta`

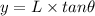
Where, L is the distance between the slit and the screen.

For small angle ,
`sin\theta=tan\theta`

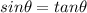
So,

Formula becomes:

`y=L* sin\theta`

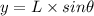
Using 1, we get:

`y=L* \frac {\lambda}{d}* m`

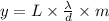
For two fringes:

The formula is:

`\Delta y=L* \frac {\lambda}{d}* \Delta m`

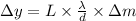
For first and second bright fringe,

`\Delta m=1`

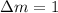
Given that:

`\Delta y=0.024\ m`

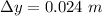
d = 2.80 mm

L = 1.20 m

Also,

1 mm = 10⁻³ m

d = 2.80×10⁻³ m

Applying in the formula,

`0.024=1.20* \frac {\lambda}{2.80* 10^(-3)}* 1`

`\lambda=5.60* 10^(-5)\ m`