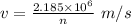Question

Derive the velocity of an electron in a hydrogen atom using Bohr's model. The electron has a mass of m, charge of (-e) and an orbit radius of r. Make sure you explain all the teps including quantization of angular momentum to get full credits

Answer 1

`v=(Ze^2)/(2 \epsilon_0* n* h)`

`v=\frac {2.185* 10^6}{n}\ m/s`

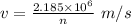
Step-by-step explanation:

According to Bohr's Theory,

The force of attraction acting between the electron and the nucleus is equal to the centrifugal force acting on the electron.

Thus,

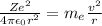`(Ze^2)/(4\pi \epsilon_0 r^2)=m_e(v^2)/(r)` ......1

Where, Z is the atomic number or the number of protons

r is the atomic radius

v is the velocity of the electron

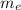`m_e` is the mass of the electron

Also,

Accoriding to Bohr, the angular momentum is quantized. He states that the angular momemtum is equal to the integral multiple of
`\frac {h}{2* \pi}`.

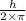`m_e vr=n* \frac {h}{2* \pi}` ....2

solving r from equation 2, we get that:

`r=n* \frac {h}{2* \pi* m_e v}`

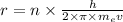
Putting in 1 , we get that:

`v=(Ze^2)/(2 \epsilon_0* n* h)`

Applying values for hydrogen atom,

Z = 1

Mass of the electron (
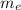`m_e`) is 9.1093×10⁻³¹ kg

Charge of electron (e) is 1.60217662 × 10⁻¹⁹ C

`\epsilon_0` = 8.854×10⁻¹² C² N⁻¹ m⁻²

h is Plank's constant having value = 6.626×10⁻³⁴ m² kg / s

We get that:

`v=\frac {2.185* 10^6}{n}\ m/s`