Question

The equation y = 0.002x - 0.30 can be used to determine the approximate cost, y in dollars, of producing x items. How many items must be produced so the cost will be no more than $387?

Answer 1

Company must not produce more than 193,650 units to keep cost as $387

Explanation:

we are given with the cost function as

y = 0.002x - 0.30

where x is the number of items produced

We are asked to determine the number of items must be produced so that the cost of production does not go beyond $387

Hence

we put y = 387 and then solve the equation thus formed for x

y = 0.002x - 0.30

387 = 0.002x - 0.30

adding 0.30 on both sides

387+0.30=0.002x

387.30=0.002x

dividing both sides by 0.002

`(387.30)/(0.002)=x`

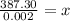
x=193,650

Company must not produce more than 193,650 units to keep cost as $387