Question

(b) The conductivity of a 0.01 mol dm–3 solution of a monobasic organic acid in water is 5.07 × 10–2 S m–1. If the molar conductance at infinite dilution (Λ°) of aqueous sodium chloride, sodium formate and hydrochloric acid are 1.264 × 10–2, 1.046 × 10–2 and 4.261 × 10–2 respectively at 25°C determine the acid dissociation constant and the pKa for the acid.

Answer 1

Step-by-step explanation:

The given data is as follows.

`\Lambda^(o)_(m)`(NaCl) =
`1.264 * 10^(-2)`

`\Lambda^(o)_(m)`(H-O=C-ONO) =
`1.046 * 10^(-2)`

`\Lambda^(o)_(m)`(HCl) =
`4.261 * 10^(-2)`

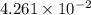
Conductivity of monobasic acid is
`5.07 * 10^(-2) S m^(-1)`

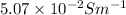
Concentration = 0.01
`mol/dm^(3)`

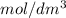
Therefore, molar conductivity (
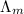`\Lambda_(m)`) of monobasic acid is calculated as follows.

`\Lambda_(m) = (conductivity)/(concentration)`

=
`(5.07 * 10^(-2) S m^(-1))/(0.01 mol/dm^(3))`

=
`(5.07 * 10^(-2) S m^(-1))/(0.01 mol * 10^(3))`

=
`5.07 * 10^(-3) S m^(2) mol^(-1)`

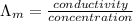
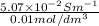
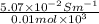
Also,
`\Lambda^(o)_(m)` =
`\Lambda^(o)_(m)_((HCl)) + \Lambda^(o)_(m)_((H-O=C-ONO)) - \Lambda^(o)_(m)_((NaCl))`

=
`4.261 * 10^(-2) + 1.046 * 10^(-2) - 1.264 * 10^(-2)`

=
`4.043 * 10^(-2) S m^(2) mol^(-1)`

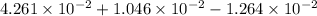
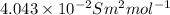
Relation between degree of dissociation and molar conductivity is as follows.

`\alpha = (\Lambda_(m))/(\Lambda^(o)_(m))`

=
`(5.07 * 10^(-2) S m^(-1))/(4.043 * 10^(-2) S m^(2) mol^(-1))`

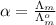
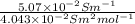
= 0.1254

Whereas relation between acid dissociation constant and degree of dissociation is as follows.

K =
`(c * \alpha^(2))/(1 - \alpha)`

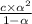
Putting the values into the above formula we get the following.

K =
`(c * \alpha^(2))/(1 - \alpha)`

=
`(0.01 * (0.1254)^(2))/(1 - 0.1254)`

=
`0.017973 * 10^(-2)`

=
`1.7973 * 10^(-4)`

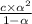
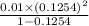
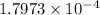
Hence, the acid dissociation constant is
`1.7973 * 10^(-4)`.

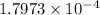Also, relation between
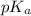`pK_(a)` and
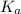`K_(a)` is as follows.

`pK_(a) = -log K_(a)`

=
`-log (1.7973 * 10^(-4))`

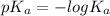
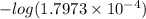
= 3.7454

Therefore, value of
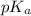`pK_(a)` is 3.7454.